רק עברו כמה ימים מאז שכתבתי פוסט על הסכנות וההטעיות בעוגות תלת מימדיות, והנה התפרסם בבלוג Junk Charts של קייזר פונג (שהוא במידה רבה ההשראה לבלוג הזה) דוגמה קיצונית אפילו יותר:
בגרף הזה, מבית ההשקעות צ'ארלס שוואב, מציג נתונים פשוטים. באמת, באמת פשוטים. הנה הנתונים הללו בעוגה פשוטה:
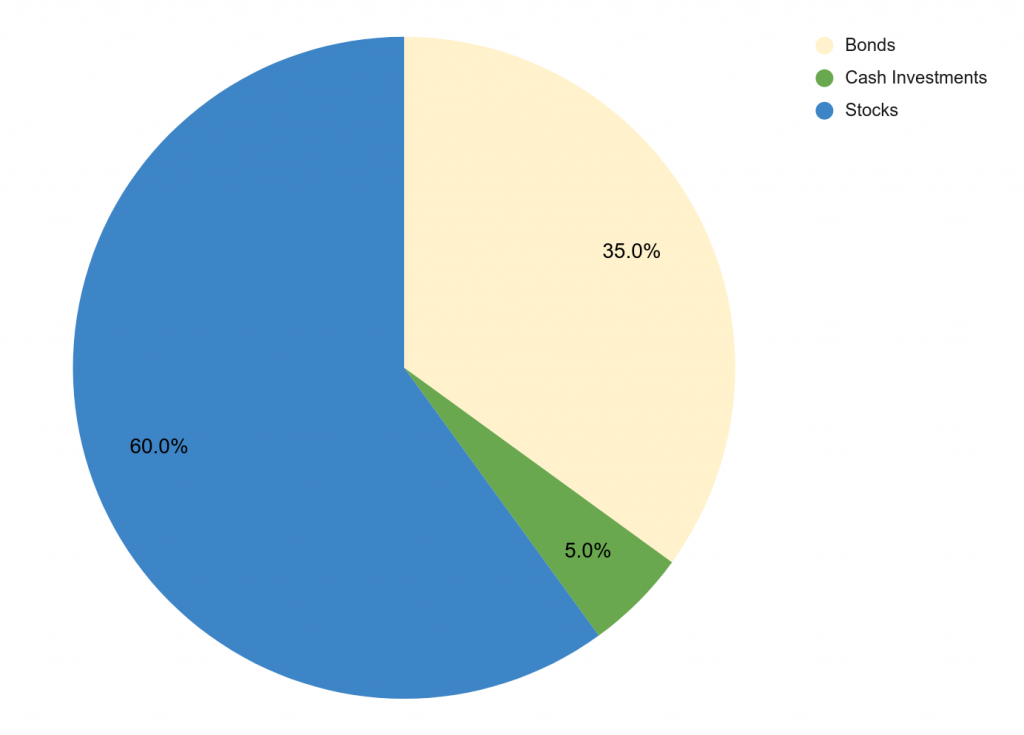
לא מסובך, נכון? שלושה פלחים, בלי יותר מדי תחכום. אבל מישהו בצ'ארלס שוואב החליט להתחכם, והפך את העוגה לתלת מימדית. אבל בניגוד לעוגה התלת-מימדית מהפוסט הקודם, שם הנפח של העוגה מוסיף משקל אקראי לפלג שבמקרה בקדמת הגרף, כאן מדובר בניפוח של פלחים ביחס ישר לנתון שלהם, מה שאומר שבעצם היחס בין פלחים מוקצן ומועצם – אם 60% הוא קצת פחות מפי 2 מ-35, אז בגרף מנופח כזה, הנפח של הפלח הזה הוא הרבה יותר מפי 2 מהמקום השני.
בחישוב מהיר וגס, בעוגה שטוחה היחס בין 35% ל-60% הוא 1.71. אבל בעוגה מנופחת, אז הפלח הגדול הוא מתוך עוגה שהיא, בסה"כ שלה, גדולה פי 1.71 מהעוגה של המקום השני. כלומר אם אני מחשב נכון (ואתם מוזמנים לתקן אותי), מדובר כאן בפלח כחול שהנפח שלו הוא פי (1.71*1.71, כלומר) 2.94 מהנפח של הפלח הבא בתור (שהוא 35% מתוך עוגה שנפחה הכולל הוא קטן יותר מהעוגה הכחולה). מיחס של קצת יותר מפי 2, הגענו ליחס של כמעט פי 3.
אז אם נחזור למנטרה שלנו – מה הבחירה האינפוגרפית הזו עושה? איזה סיפור היא מעבירה? הסיפור שהיא מעבירה הוא של הקצנת הפערים. בדומה לקיצוץ בסיס מערכת הצירים, זו בחירה (מודעת או שלא) שלוקחת את הנתונים הגולמיים ומספרת סיפור שמקצין את ההבדלים בין הנתונים, בניגוד לסיפור שמטשטש את ההבדלים. האם זה ברור מהגרף שזה מה שהוא עושה? לא, אני לא חושב שזה מוצהר במפורש. וזה מה שהופך את הגרף, במודע או שלא,למניפולטיבי.
אני חושב שבחרו בגרף התלת־ממדי כדי לייצג את העובדה שההשקעה האבסולוטית במזומן ובאגרות חוב זהה בשני הגרפים (גובה כל פלח אמור לייצג את ההשקעה האבסולוטית בו). זה לא היה אפשרי עם שני גרפי עוגה פשוטים, גם אם אחד מהם היה קטן מהאחר. אבל זה לא ממש עובד, כי השינויים בשטחים האפורים והירוקים גדולים ומסתירים את העובדה שמרכזי העוגות שלהם נשארים באותו קו גובה.
אולי היה אפשר לעשות את זה עם שני גרפים שבכל אחד מהם עמודה מחולקת לשלושה חלקים, שני החלקים התחתונים של העמודה זהים בשני הגרפים, והעליון קצר יותר בגרף הימני, כך שהגרף הימני נמוך מהשמאלי. גם זה לא נהדר, אבל מי שמתעקש לשלב נתונים יחסיים ואבסולוטיים אינו רשאי לצפות לתוצאה נהדרת.